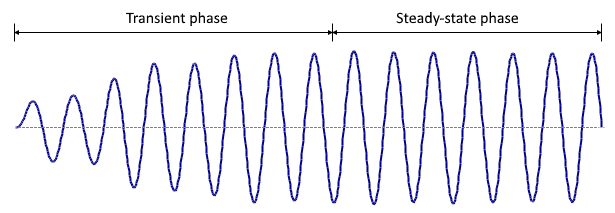
When the structure begins responding to the harmonic
loads it goes through an initial "transient phase" during
which it moves in an irregular way while it "catches up"
with the vibrating load sources. It then reaches a steady oscillating
motion called its "steady-state phase". A harmonic analysis
is concerned just with the steady-state phase of the structure's response.
If you are interested in the transient phase or if your vibrating
loads are not harmonic then you should run a transient
response analysis instead. Note that the amplitude of the oscillations
in the transient phase can exceed those of the steady-state phase.
Supported harmonic load types are "Applied loads"
(vibrating masses at nodes), "Base displacement", "Base
velocity" or "Base acceleration" (support nodes vibrating
in-phase).
Each load source is assumed to be vibrating in a sinusoidal
(harmonic) motion with a user specified frequency and phase.
Load sources operating at different frequencies and
phases can be combined within a harmonic load case.
Harmonic result load cases can be combined with static
and other load case types using combination load cases.
Damping can be taken into account and applied as either
"Modal" or "Rayleigh" damping, or it can be disabled.
You can choose between "Time sampling" or
"Frequency sampling". Time sampling evaluates how the structure
responds over a specified period of time (ie. a time-history response),
whereas frequency sampling evaluates how the structure responds to
a specified range of frequencies (ie. a frequency response). Frequency
sampling allows you to display a resonance curve that shows the effect
of each frequency on the excitation of the structure.
You can choose the time or frequency range and the
number of steps over that range at which calculations are done.
When frequency sampling is used, you can define and
apply a "Factor versus frequency table" that allows you
to change the magnitude of the applied loads as the frequency changes.
After a harmonic response analysis, the model can
be animated to show how it responds to the harmonic loads.
Displacement, velocity, acceleration and phase diagrams
can be displayed for any nodes in the structure. These are time-history
curves if time sampling is used or resonance curves if frequency sampling
is used.
Each time or frequency step (or just selected steps)
can be converted to result load cases that contain displacements,
forces, moments, stresses and reactions, just like you would get from
a static analysis. You can show diagrams or get reports for these
load cases or use them in the normal way in any of the design modules.