Running a buckling analysis
You can run a buckling analysis by selecting "Buckling Analysis" from the Analysis menu.
The input data requirements for a buckling analysis are the same as those for a static analysis. No extra buckling data is required.
You do not have to run a static analysis before a buckling analysis.
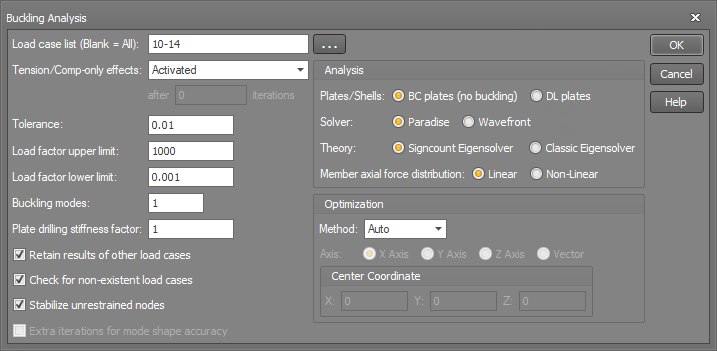
Load case list
If you want to analyse all load cases then this field can be left blank, otherwise you should type in a list of load cases (separated by commas or dashes) that you want analysed.
For the fastest analysis time you should generally analyse only the load cases that can occur in reality. For example, there is no point in analysing a live load case on its own because it can't occur in real life without being combined with dead load. This means that you should generally analyse just the combination load cases and not the primary load cases that the combinations are made from.
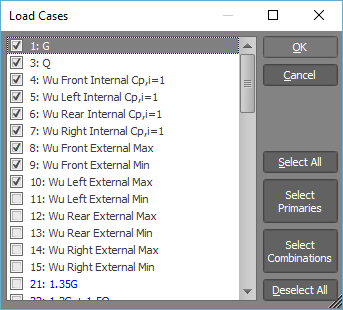
When specifying the load case list, you can either list them directly or you can click the ![]() button to display and select from a
list of the load cases currently in the job as shown below.
button to display and select from a
list of the load cases currently in the job as shown below.
Tension/Comp-only effects
Refer to "Tens/comp-only effects" in the static analysis solver.
Tolerance
Note that this setting only affects the "Signcount Eigensolver".
This controls the accuracy to which the buckling load factors will be calculated. For example, a tolerance of 0.01 means that the load factors will be within +/- 0.01 of the exact value. Each extra decimal place in the tolerance will increase the number of iterations per mode by 3 or 4. For example, a tolerance of 0.001 will require 3 or 4 more iterations per mode than a tolerance of 0.01.
Load factor upper limit
The upper limit above which the analysis will no longer search for buckling load factors. Once this limit is reached, the analysis will stop, even if not all requested buckling modes have been calculated.
Load factor lower limit
The lower limit below which the analysis will not search for buckling load factors.
Buckling modes
The number of buckling modes (in ascending order) that are required. Normally only the first buckling mode is of interest, because beyond that the structure has usually collapsed and further modes are of academic use only.
If the first buckling mode is caused by local buckling of a slender element or group of elements rather than the structure as a whole, the model should be changed so that overall structure buckling occurs instead. One way of achieving this could be to change the slender members into tension-only members so that they become disabled rather than buckle (see also Members).
You should view the buckling mode shapes graphically to determine whether or not overall buckling of the structure has occurred.
Plate drilling stiffness
Refer to "Plate drilling stiffness" in the static analysis solver.
Retain results of other load cases
If you have specified that not all load cases are to be analysed and, if results already exist for some of the non-specified load cases, you can choose to retain them or have them deleted.
Check for non-existent load cases
If you have defined combination load cases that contain other load cases which don’t yet exist, this option will detect and report them. It is optional because some users prefer to have a standard set of combination load cases that contain primary load cases which are just ignored during the analysis if they don’t exist.
Stabilize unrestrained nodes
Nodes that are free to rotate or translate in one or more directions without resistance from interconnecting members, restraints or constraints can be automatically restrained during the analysis so that instabilities don’t occur.
For example, if a node was connected to a number of members, all of which were pin-ended, a rotational instability would normally result due to the unrestrained rotation of the node. However, the stabilize option would apply a temporary rotational restraint to the node during the analysis, preventing an instability.
Although this solves many instabilities, it doesn’t fix them all, and the prevention of non-trivial instabilities is still dependent on good modelling practice.
Note that if any node loads (forces or moments) have been applied directly to an unstable degree of freedom that has been stabilized with this option, the applied node load would go into the temporary restraint rather than into the structure. Using the above example again, if a node was connected to a number of members that were all pin-ended and the stabilize option had applied a temporary Z rotational restraint to that node, any Z moment applied directly to that node as a node load would go straight into the temporary restraint rather than into the structure.
Extra iterations for mode shape accuracy
Note that this setting only applies when using the "Signcount Eigensolver" theory.
The buckling analysis is complete when the buckling load factor has reached the desired accuracy (as specified by the tolerance), however it is possible that at this point the buckling mode shapes are not totally accurate. Mode shape accuracy can be achieved by turning on the "Extra iterations for mode shape accuracy" option, however because buckling mode shapes are only used as a visual aid to assess the buckling location and its shape then the extra iterations and analysis time involved is not usually warranted.
Plates/Shells
You can choose between "BC" (linear only) elements or "DL" (linear or non-linear) elements. "BC" elements are identical to the ones used in SPACE GASS 12.91 and earlier versions, whereas "DL" elements are new and can be used to model non-linear effects and plate/shell buckling.
"BC" elements use the well known Kirchoff or Mindlin linear plate theories, depending on which type is selected in the input data. They always behave linearly, even during a non-linear static analysis.
"DL" non-linear elements are based on the large-strain/large-deflection version of the Reissner-Mindlin shell theory that takes into account the 2nd order strain terms, stress stiffening, large displacements and large rotations (ie. full large-displacement non-linear theory), whereas "DL" linear elements use a small-displacement/small-strain linear version of the Reissner-Mindlin shell theory. "DL" elements always use Reissner-Mindlin theory regardless of whether you select Kirchoff or Mindlin in the input data.
Because "BC" plate/shell elements do not buckle, you should always use "DL" elements in a buckling analysis if you want the plates/shells to contribute towards the buckling behaviour.
If you want to perform an analysis that is identical to SPACE GASS 12.91 and earlier versions then you should choose "BC" elements, a drilling stiffness factor of -S (where S is the plate drilling stiffness used in SPACE GASS 12.85, 12.90 or 12.91) and a plate shear thickness that is 6/5 of the shear thickness used in SPACE GASS 12.85, 12.90 or 12.91 (because the shear thickness is now factored by 5/6 internally during the analysis).
Solver
The "Paradise" solver is a new parallel multi-core sparse solver that fully utilizes the multiple cores in a modern computer's CPU. All of the available cores are run in parallel to get the maximum possible analysis speed. It also takes full advantage of the sparseness of the structural matrix during the solution to minimize memory requirements and further increase the speed.
Because of its speed, the Paradise solver is the recommended option, however one current restriction is that if used with the "Signcount Eigensolver" theory then it doesn't generate buckling mode shapes and so if mode shapes are essential then you should use the "Classic Eigensolver" theory or the "Wavefront" solver instead. Note that buckling mode shapes are for visual purposes only and do not affect the calculation of the buckling load factor, the member effective lengths or any of the other modules that use the buckling analysis results.
The "Wavefront" solver also takes into account the sparseness of the matrix but doesn't run in multi-core mode. It is generally slower than the Paradise solver and can be used if the Paradise solver is unable to obtain a solution or if you require buckling mode shapes.
Both solvers should yield virtually identical results.
Note that the "Watcom" solver is the one used in pre-SPACE GASS 12 versions. It has been superseded by the Paradise and Wavefront solvers which are both significantly faster.
Theory
You can choose between the "Signcount Eigensolver" and the "Classic Eigensolver" theories. Each one has distinct advantages and disadvantages.
The "Signcount Eigensolver" theory uses the method presented by Wittrick and Williams (12) in which the number of negative terms in the diagonal of the structure stiffness matrix (the sign count) is determined after a forward Gaussian decomposition. The sign count indicates how many buckling modes have been exceeded by the current loading level. This method is extremely accurate and isn't usually affected by whether members have been subdivided or not. It is the method that SPACE GASS 12.91 and all earlier versions use. The disadvantage is that it can't be used to model plate/shell buckling, even with the new "DL" plates.
The "Classic Eigensolver" theory solves the well known Eigen equation (Ko + λiKg) Ui = 0, where Ko is the structure's initial stiffness matrix, Kg is the geometric stiffness matrix, λi is the eigenvalue (buckling load factor) for mode i and Ui is the eigenvector (buckling mode shape) for mode i. It works with members and plates/shells, and is typically the method used in other structural analysis programs. The main disadvantage is that it tends to overestimate buckling load factors, although this can usually be improved by subdivision of members or finer meshing of plates/shells.
Neither theory works particularly well when the structure contains cable members, although the "Signcount Eigensolver" theory produces accurate results if the buckling load factor is close to 1.0. For further information on this, refer to the procedure outlined in "Buckling analysis with cable members". The "Classic Eigenvalue" theory does not give accurate results when cables are present in the model.
If your model contains both plates/shells and cable members then neither theory is particularly suited. You may consider using the "Signcount Eigenvalue" theory initially, taking note of the special treatment of cables mentioned in " Special buckling considerations" and being aware that buckling of the plates/shells in your model will not be considered. You could then try the "Classic Eigensolver" theory to see if buckling of the plates/shells occur at a lower load than member buckling and if any plate/shell buckling plays any significant role in the overall buckling of the model.
If you unsure of whether a buckling analysis has produced accurate results, you can check it by running a non-linear static analysis with the "Perform structure buckling check" option ticked. In the static analysis you should choose the same type of plates/shells as you used in the buckling analysis and you should select "Small" displacement theory. For example, if the buckling analysis of load case 10 produced a buckling load factor of 2.4 and you wanted to verify that this wasn't overestimating the structure's buckling capacity, you could create a new combination load case that factored up load case 10 by close to 2.4 (say 2.3) and then run a non-linear static analysis on it. If no buckling message appeared at the end of the analysis then you could be confident that the buckling load factor was at least 2.3. The structure buckling check in the non-linear static analysis is very reliable, even if the model contains cables.
Optimization
Refer to "Optimization" in the static analysis solver.
Axial force distribution
Note that this setting only applies when using the "Signcount Eigensolver" theory.
The buckling properties of a structure are largely dependent on the axial force in the members. The buckling analysis module performs its own static analysis first to determine the axial force distribution and you can nominate either linear or non-linear for this initial static analysis phase. Generally, the choice between linear or non-linear doesn't significantly affect the buckling load factor and, because linear is faster, it is recommended for most frames. Naturally, some structures, such as those containing cable members, which cannot be analysed linearly, require you to select non-linear.
When all of the information has been entered, the buckling analysis module calculates the buckling load factor and mode shapes for each load case and then saves them ready for graphical or text report output.
If you want to terminate the analysis before it is finished, just press ESC or the right mouse button.
![]() Because plates are linear elements, they will not buckle regardless of the load applied.
Because plates are linear elements, they will not buckle regardless of the load applied.