Plate strips

Plate strips can be drawn anywhere across a surface that has been modelled with plate elements, and then displacement diagrams, bending moment diagrams, shear force diagrams, axial force diagrams and stress diagrams can be displayed along the strip. Strips can have a uniform width or can be tapered. For detailed information about plate strips refer to "Plate strip data".

Creating a new plate strip

In order to create a new plate strip you can either click the plate strip draw button in the top toolbar or from the Structure menu select "Plate strips" => "Draw Plate Strips". It is then just a matter of drawing the strip between two nodes that define its ends. The plane of the strip is defined by the plane of the plate element attached to the strip's start node. If there is more than one plate element attached to the start node then you can select the one you want to use by hovering over it until it highlights before you click the start node to start drawing.

New strips default to a width of 1m if metric units are used or 3ft if Imperial units are used, and so after drawing a strip you should edit it to change the width, offsets and other parameters to suit your exact requirements.

Editing a plate strip

You can edit a plate strip either by double-clicking it or by selecting it and then right-clicking followed by selecting "View/Edit Plate Strip Properties (Form)" from the popup menu that appears. The plate strip properties form that appears below is fully explained in "Plate strip data".

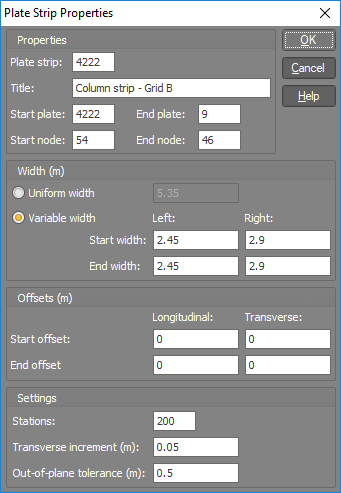
Viewing plate strips

You can view plate strips by clicking the "Show Plate Strips/Cuts" button near the top of the side toolbar. By default the strip centerline and its width are shown visually, however you can also show strip profiles (cross sections) by clicking the arrow next to the main button.

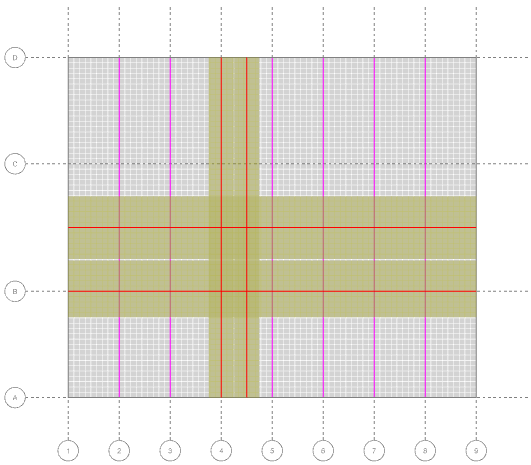
The following image shows typical column and middle strips drawn in two directions on a reinforced concrete slab.

Analysis diagrams

If plate strips are visible then you can show their displacement, bending moment, shear force, axial force and stress diagrams by clicking the desired , , , or button on the side toolbar. The bending moments, shear forces, axial forces and stresses along the strip are calculated by aligning and integrating the values from the underlying plate elements, whereas the displacements are obtained from the maximum of the displacements across the width of the strip at each station along the strip.

Out-of-plane and in-plane shear force diagrams are selectable via the and buttons, where the button shows out-of-plane shear forces and the button shows in-plane shear forces.

Wood-Armer bending moment adjustment

In order to take into account the effect of twisting on the bending moments in the strip, a bending moment diagram adjusted using the Wood-Armer method can also be displayed. Depending on the twisting moment, the Wood-Armer adjustment generally increases the positive and negative moments. The procedure for adjusting My (the moment about an axis across the strip) is as follows:

1. For each station along the strip the Mx, My and Mxy values are summed from the plate elements across the strip to obtain a single Mx, My and Mxy value at the strip station.

This has the effect of amplifying the positive and negative moments. For more information refer to "Sign conventions".

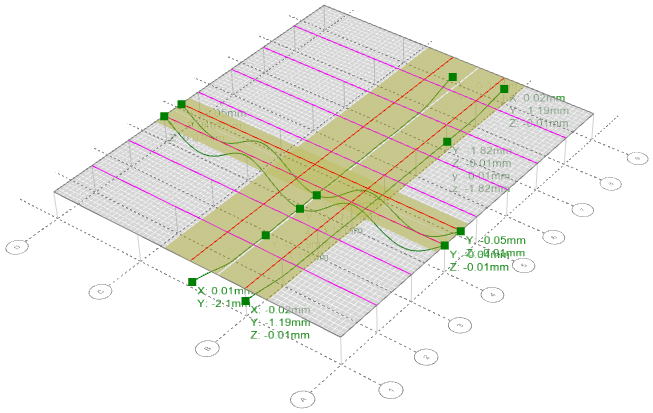
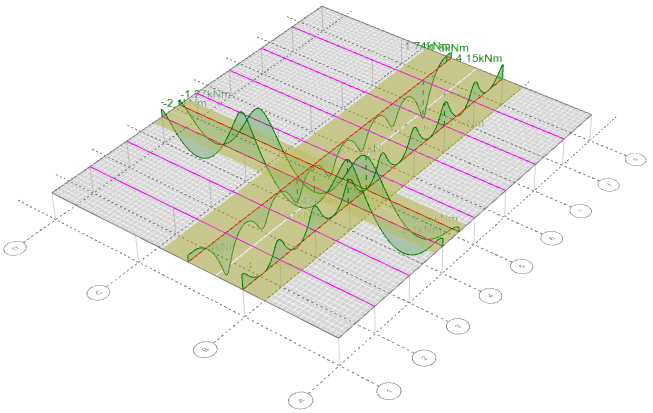
The following diagrams show examples of deflections, bending moments and shear forces.

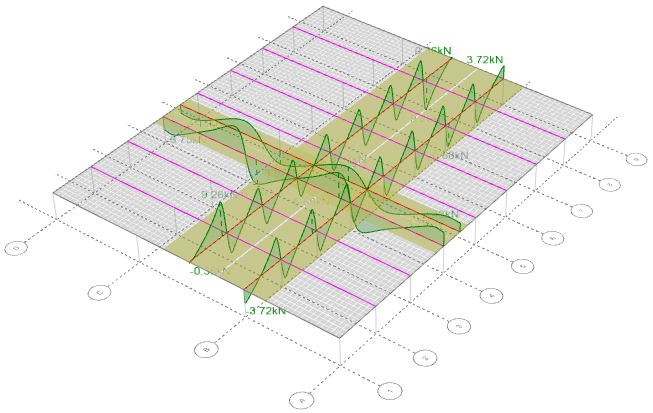
Smoothing Analysis Diagrams

If smoothing is turned off then the plate strip values are calculated based on the raw plate element data.

This usually results in strip diagrams that have some stepping in them rather than being smooth curves. If smoothing is turned on then interpolation is performed between the plate element values, resulting in much smoother plate strip diagrams. It is a good idea to compare the smoothed and unsmoothed diagrams to ensure that their values are comparable. If there is a significant discrepancy between the smoothed and unsmoothed diagrams then in most cases it is safer to use the unsmoothed values.

If you see unexpected peaks or jumps in a plate strip diagram then this could indicate that the transverse increment needs to be reduced in order to provide more data sampling points for the diagram. This can be particularly evident in diagrams that aren't smoothed.

Underestimation of peak bending moments and bending stresses

When viewing plate strip bending moment or bending stress diagrams, because they are calculated from just one value per plate element, the moments and bending stresses at the very ends of the strip may be underestimated if the ends of the strip coincide with the edges of the wall or slab being modelled. This is because the end values are based on results that come from half a plate element width in from the ends.

Consider the following example which shows a slab strip modelled with plate elements and supported on columns at each end.

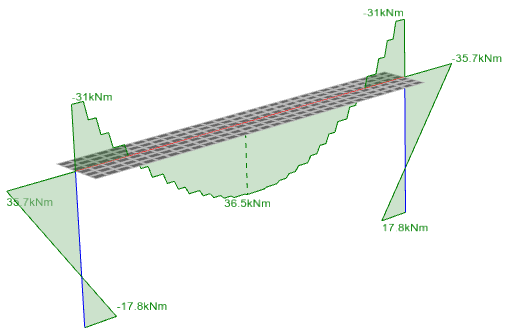
The bending moment diagram is unsmoothed and that's why you can see steps in the diagram that coincide with the rows of plate elements. You can also see that the end moments in the strip are underestimated compared to the column moments. This is because bending moments are only available at the center of each plate element rather than the edges. Turning on smoothing will remove the stepping, however it won't solve the problem of the end moments being underestimated.

One solution to this is to tick the "Extrapolate End Moments and Bending Stresses" option to have the end values extrapolated based on values from plate elements that are further in from the ends.

The following diagrams show the effect of smoothing and extrapolating on the above example.

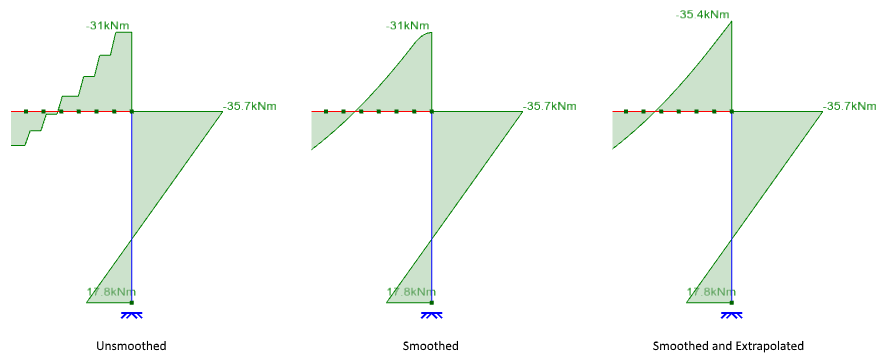
You can see that extrapolating the end values gives a very good result in this case, however you must always check after extrapolating to make sure that the adjusted end values look correct before you rely on them or use them in a design.

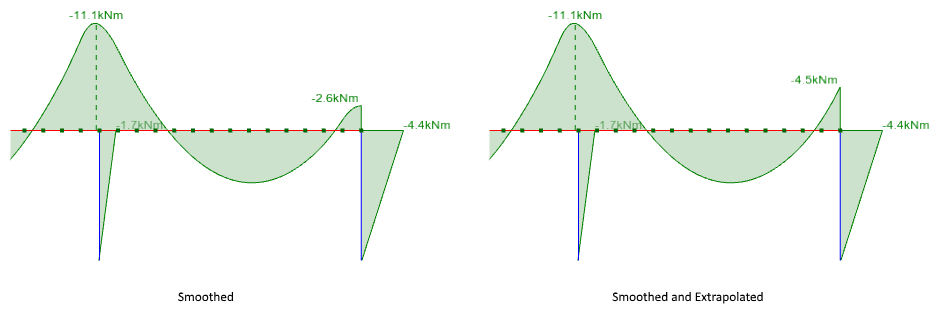
Note that a similar underestimation of peak bending moments can also occur away from the ends where a column or beam provides support to an internal point along the plate strip. However as you can see below, while extrapolating greatly improves the end values, it does not change the internal peak bending moments.

In order to improve the accuracy of internal peak moments (or end moments if extrapolation doesn't work well) the solution is to refine the plate mesh around the problem areas. The diagram below shows the result of reducing the mesh size at the internal support and ends.

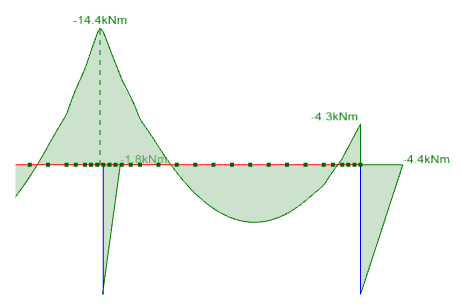
It is strongly recommended that you always check the plate strip bending moment and bending stress diagrams carefully and then use smoothing, extrapolation and/or refined meshing if necessary to achieve accurate results. Don't just use the plate strip diagrams without checking them first.

Multiple load cases

If multiple load cases are selected then a separate plate strip diagram is shown for each load case. If enveloping is turned on then the plate strip diagrams show the minimums and/or maximums from the selected load cases.

Out-of-plane tolerance

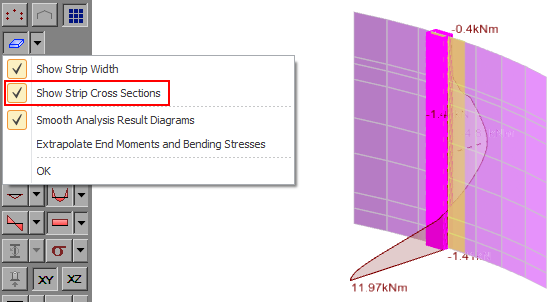
The "Out-of-plane" tolerance setting is very important to get right if you have a plate strip on a surface that isn't completely flat. In the following example we have a 1m wide vertical plate strip on the wall of a circular tank for which the contour diagram is indicating a moment at the bottom of 21.77 kNm/m. For our 1m wide strip we are expecting a moment at the bottom of 21.77 kNm, but the bending moment diagram is showing only 11.97 kNm, about half of what we are expecting.

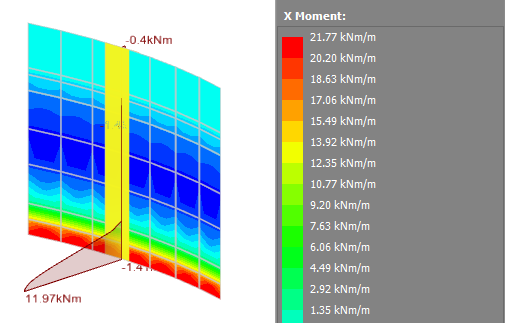
If we turn on the plate strip cross sections you can see that only half of the strip is active, indicating that not all the underlying plate elements are contributing to the bending moment diagram. In this case it is occurring because the plate elements in one half of the strip are in a slightly different plane to the ones in the other half due to the curvature of the tank wall.

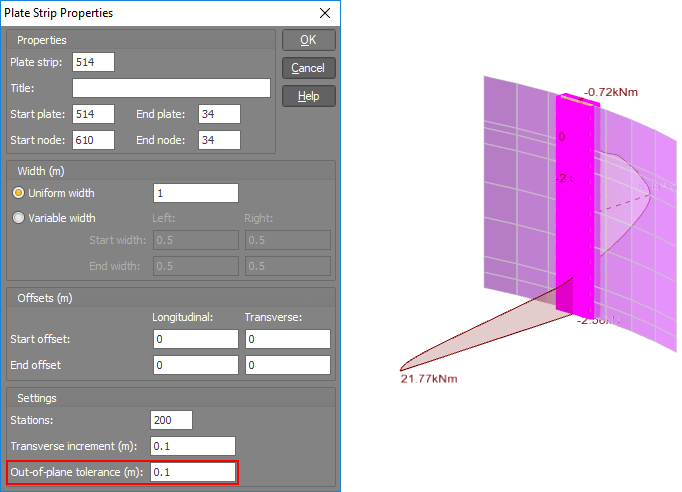
If we increase the out-of-plane tolerance to allow for this then the plate strip shows the expected result.

This illustrates that when you have a plate strip on a surface that isn't completely flat, it is very important that you turn on the strip cross sections to check that all of the strip is active before you accept its results.